Вы не правы. О движении 3-х мерного объекта в плоскости можно и нужно говорить. Во многих областях науки и техники 3-х мерный предмет сводят к точке в пространстве, совпадающей с центром масс объекта или с его геометрическим центром, в зависимости от целей.
но точки все эти движутся по параллельным траекториям. Например для робота, которого мы хотим научить копировать эти движения Важно будет на 1-м этапе не ошибиться при приближении к стеклу, а затем осуществлять перемещения исключительно в одной плоскости, параллельной стеклу. И уравнения описывающие эти движения будут для плоскости, а не для пространства.
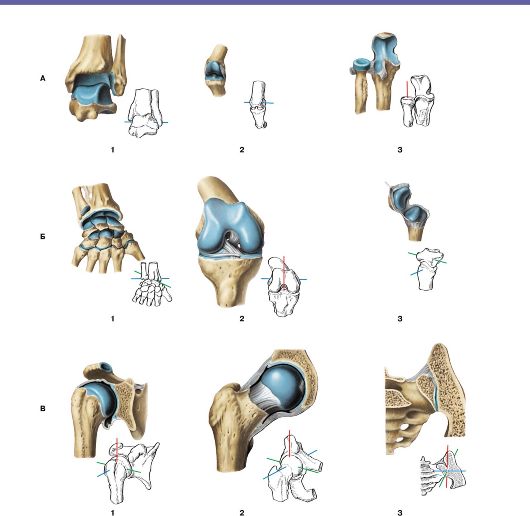
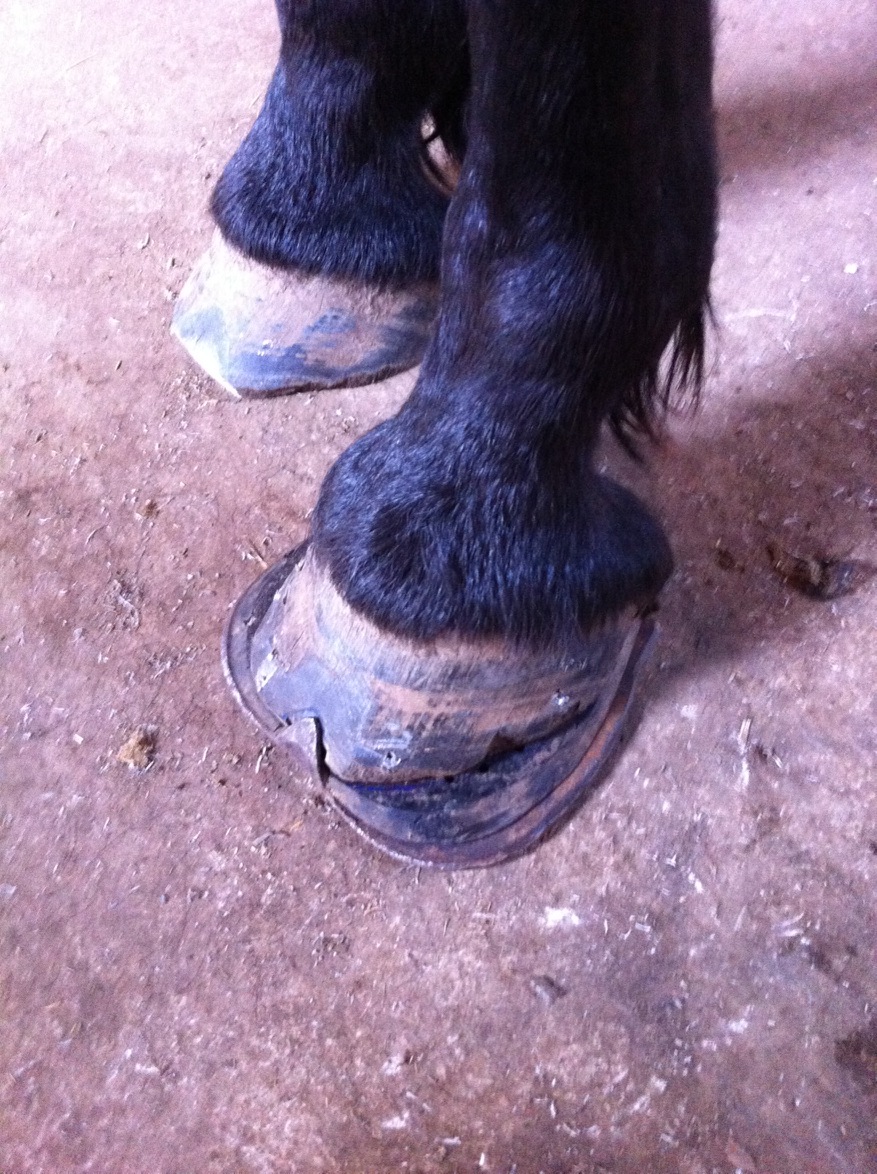
движение вокруг оси абсолютно не отменяет параллельное с ним движение в плоскости и наоборот. Поэтому нельзя говорить что одно более верно чем второе. Там все в комплексе. Например копыто движется и вокруг венечного и вокруг путового и вокруг запястного и даже локтевого суставов и весь этот комплекс вращательных движений складывается в том числе и в поступательное движение копыта относительно земли.